Wason selection task, also known as the four-card problem, is a well-argued topic of psychology, surveying how human reasoning works. A typical example is here.
There are four cards on the table. For each card, an alphabet is on one side, and a number is on the other. You can see four cards on the table, A, K, 4, and 7.
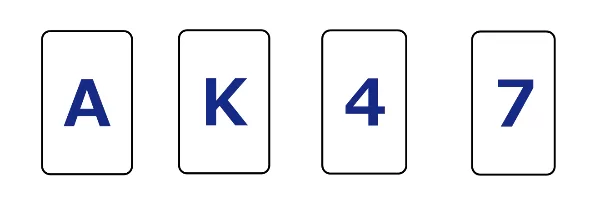
You are going to check the rule "if one side of the card is a vowel, then the other must be an even number." is true or not. Which card(s) will you turn over?
Caution: The main topic is how people think and why human reasoning sometimes goes wrong.
(Hereafter, "if one side of the card is a vowel, then the other must be an even number." is referred to as Rule X.)
Logical answers will be A and 7. Rule X prohibits a vowel and an odd number on the same card. The rule is not true if the other side of A is an odd number. So you need to check the "A" card. The rule is not true if the other side of 7 is a vowel. So you need to check the "7" card.
Many people choose A and 4.
Many people choose A and 4, but the "4" card is irrelevant to check whether Rule X is true or false. Checking the "4" card confirms the already known fact that the "4" card matches Rule X. This tendency is an example of "confirmation bias."
Updated:

